f(Z) es analitica en Zo si solo si f es derivable para todo Z de algun disco D:|Z-Zo|< r
PROPIEDADES
1. Si f(Z)=u(x,y)+iv(x,y), analitica en algun dominio entonces u ^ v satisfacen las Ecuaciones de Cauchy- Rieman para todo (x,y) del dominio.
2. Si u(x,y)^ v(x,y) y sus primeras derivadas parciales son continuas y ademas cumplen las ECR, la funcion f(Z) es analitica.
3. Sea f(Z) analitica en un cierto dominio, entonces u^v son armonicas, es decir cumplen:
FUNCIONES TRIGONOMETRICAS
FUNCIONES HIPERBOLICAS
FUNCIONES LOGARITMICAS
INTEGRACION EN EL PLANO COMPLEJO
- Se aplican las reglas y propiedades de la integracion de funciones reales salvo el caso de funciones que son eminentemente complejas, tales como |Z|; Z conjugado, en las cuales se debe aplicar propiedades y teoremas especificas.
- En el caso de integrales indefinidas (antiderivadas ) de funciones analiticas se mantiene la analogia con las funciones reales: sin embargo se presentan ciertas diferencias debido a:
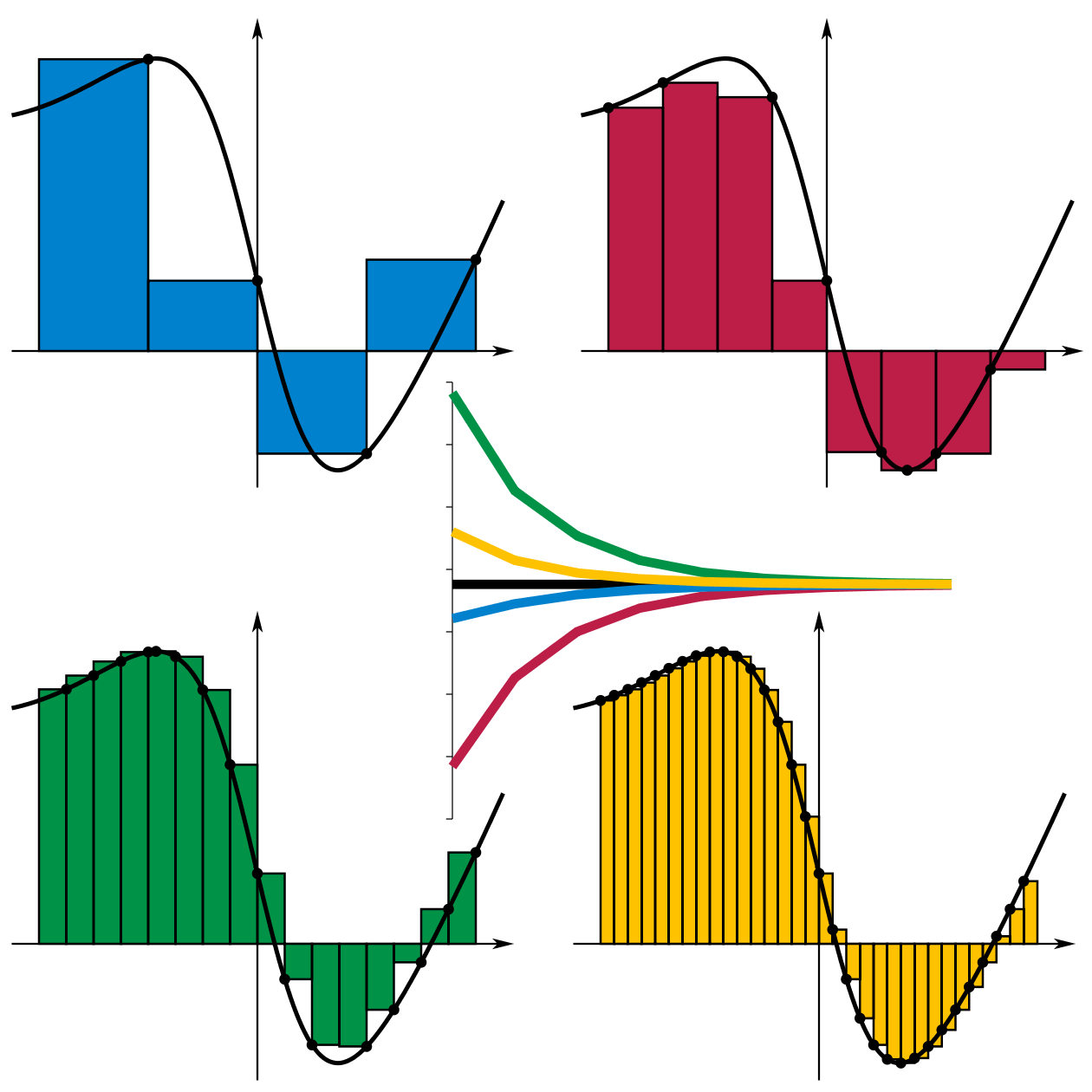
1. Los numeros reales se representan en el eje de las x y las integrales se entienden como una aproximacion de las sumas de Riemann.
INTEGRALES INDEFINIDAS

CURVAS EN EL PLANO








A partir del teorema de Cauchy-Goursat, se pueden demostrar proposiciones como la siguiente:
 Sea ƒ(z) analítica sobre C, siendo C un contorno cerrado simple, y en el interior de C. Si se toma un punto interior "
Sea ƒ(z) analítica sobre C, siendo C un contorno cerrado simple, y en el interior de C. Si se toma un punto interior "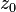 " de C, se cumple que:
" de C, se cumple que:
Ejemplo sencillo
- Se aplican las reglas y propiedades de la integracion de funciones reales salvo el caso de funciones que son eminentemente complejas, tales como |Z|; Z conjugado, en las cuales se debe aplicar propiedades y teoremas especificas.
- En el caso de integrales indefinidas (antiderivadas ) de funciones analiticas se mantiene la analogia con las funciones reales: sin embargo se presentan ciertas diferencias debido a:
1. Los numeros reales se representan en el eje de las x y las integrales se entienden como una aproximacion de las sumas de Riemann.

2. Los numeros complejos se representan en el plano complejo lo cual nos lleva a considerar integrales de linea sobre una curva C sobre el plano complejo en lugar de la sumas de Riemann
3. En las integrales cerradas e presentan propiedades novedosas y que solo se cumplen para las funciones de variables compleja asi como por ejemplo. La integral de Cauchy.
INTEGRALES INDEFINIDAS
Sea
F'(z)=f(z), entonces:
Siendo
c Є C, constante de integración.
CURVAS EN EL PLANO
Una curva g en el plano C=R x R de puntos (x, y) tal que:
- Z(a)^Z(b) son los puntos extremos de la curva.
- Si Z(a)^Z(b) coinciden, se dice que la curva g es una curva cerrada.
- El sentido positivo de la curva g sera aquel en el que t aumenta.
- Si Z(a)^Z(b) coinciden, se dice que la curva g es una curva cerrada.
- El sentido positivo de la curva g sera aquel en el que t aumenta.
Donde x y y
son funciones continuas que depende de "t".
DEFINICIÓN:
Sea z una función continua tal que:

Sea z una función continua tal que:
Es una
curva, se dice que la curva es diferenciable si la derivada de z es diferente
de 0 para todo t que pertenece al intervalo de:

INTEGRALES DE LINEA
PROPIEDADES
Sean f(z) y g(z) funciones de variable compleja continuas a trozos sobre un contorno c descrito por la ecuacion z=z(t)( )
)
INTEGRALES DE LINEA
INTEGRALES DE CAUCHY
Si f(z) es analítica en un dominio simplemente conexo D y su derivada es continua en D entonces para cualquier contorno cerrado simple contenido en D se tiene:
- El teorema sigue siendo válido cuando el contorno C no es simplemente conexo pero tiene un número finito de "agujeros".
- Sea C un contorno simple cerrado, y sean Cj (j=1, 2, ..., n) un número finito de contornos simples cerrados dentro de C, tales que las regiones interiores a cada Cj no tengan puntos en común. Sea R la región cerrada formada por todos los puntos dentro de C, salvo los puntos interiores a cada Cj. Denotamos por F toda la frontera orientada de R formada por C y todos los contornos Cj, recorridos en un sentido tal que los puntos interiores de R queden a la izquierda de F. Entonces, si f es analítica en todo R,
A partir del teorema de Cauchy-Goursat, se pueden demostrar proposiciones como la siguiente:
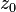 " de C, se cumple que:
" de C, se cumple que:

No hay comentarios:
Publicar un comentario