Febrero

PRIMERA SEMANA

 En la primera clase se nos dio una breve explicacion de lo que se va a realizar en el transcurso del curso que se va a realizar.

 Tambien se nos dio a conocer cuales son las tareas que se nos van a encomendar para ser cumplidas.

 Segunda Clase

 Introduccion a los numeros complejos

 Que es un numero complejo?



Los números complejos son una extensión de los números reales y forman el mínimo cuerpo algebraicamente cerrado que los contiene. El conjunto de los números complejos se designa como C, siendo R el conjunto de los reales se cumple que RϲC. Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i), o en forma polar.

REPRESENTACION GRAFICA

 OPERACIONES CON NUMEROS COMPLEJOS


 Definiremos cada complejo z como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), en el que se definen las siguientes operaciones:
  • Suma
(a,b)+(c,d)=(a+c,\,b+d)
  • Producto por escalar
r(a,b)=(ra,\,rb)
  • Multiplicación
(a,b)\cdot (c,d)=(ac-bd,ad+bc)
  • Igualdad
(a,b)=(c,d)\iff a=c\land b=d

 A partir de estas operaciones podemos deducir otras como las siguientes:
  • Resta
(a,b)-(c,d)=(a-c,\,b-d)
  • División
{\frac {(a,b)}{(c,d)}}={(ac+bd,\,bc-ad) \over c^{2}+d^{2}}=\left({ac+bd \over c^{2}+d^{2}},{bc-ad \over c^{2}+d^{2}}\right)

 Al primer componente (que llamaremos a) se le llama parte real y al segundo (que llamaremos b), parte imaginaria. Se denomina número imaginario puro a aquel que está compuesto sólo por la parte imaginaria, es decir, aquel en el que a=0 .

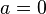  • Conjugado                 {\bar {z}}=a-{\mathrm {i}}b\Longleftrightarrow z=a+{\mathrm {i}}b  



SEGUNDA SEMANA

Se aprendio a cerda ce Modulo de un complejo que es :

|z|={\sqrt {zz^{*}}}={\sqrt {{\hbox{Re}}^{2}(z)+{\hbox{Im}}^{2}(z)}} 

 Forma trigonometrica de un numero complejo



  • Cálculo de módulo y argumento de un complejo

 

Para calcular el argumento de un número complejo z = a + bi , basta con tener en cuenta que:

 

                                           a = |z|·cos a

                                           b = |z|·sen a

 

Dividiendo estas dos igualdades,

 

                                       

 


 

Entre 0º y 360º hay, en general, dos ángulos cuya tangente toma ese valor. Para decidirse entre ellos es preciso fijarse en qué cuadrante se encuentra el complejo en cuestión.

 

Para calcular el módulo se suman los cuadrados de las dos igualdades obtenidas:

 

                                a2 + b2 = |z| cos a + |z|2 sen a =

                                                = |z|2 (cos a + sen a) = |z|2 Þ
                                          



a + bi  = cos a + sen ai  = ( cos a + i sen a)

  • Producto de complejos en forma módulo-argumental
 

Aunque ya se dispone de un método para calcular el producto de dos números complejos cualesquiera, cuando ambos números vienen dados en su forma módulo-argumenal existe un procedimiento mucho más sencillo. Este método consiste en multiplicar sus módulos y sumar sus argumentos.

 

Para ver que esto es correcto, basta con efectuar la multiplicación:

 

                    Ra · R'a' = R (cos a + i sen a) · R' (cos a' + isen a' ) =

    = RR' { (cos a · cos a' - sen a · sen a' ) + i ( sen a · cos a' + cos a · sen a' )}

 

Pero las expresiones que se encuentran entre paréntesis son precisamente las
               Ra · R'a' = RR' {cos (a + a') + i sen ( a + a' )} = (RR' )a + a'
  • Division
La división de dos números complejos es otro número complejo tal que:

Su módulo es el cociente de los módulos.

Su argumento es la diferencia de los argumentos.


cociente 

  •  Potencias

La potencia enésima de número complejo es otro número complejo tal que:

Su módulo es la potencia n-ésima del módulo.

Su argumento es n veces el argumento dado.

potencia

(230°)4 = 16120°


  • Fórmula de Moivre

Fórmula de Moivre


  • Raíz

raíz 

La raíz enésima de número complejo es otro número complejo tal que:

Su módulo es la en raíz enésima del módulo.


módulo

Su argumento es:

argumento

k = 0,1 ,2 ,3, … (n-1)
TERCERA SEMANA

 LOGARITMOS EN COMPLEJOS
Se define el logaritmo de un complejo como la operación inversa de la exponencial.

PROPIEDADES

RESUMEN
FUNCIONES DE VARIABLE COMPLEJA

Recordemos que una función real f de variable real sobre un conjunto de números reales es una función que asigna a un número real x ∈D otro número real y = f(x).
Este concepto se generaliza fácilmente al caso complejo:

El conjunto D se llama, igual que en el caso de las funciones reales,dominio de f. Igualmente, el conjunto de las imágenes de f se llama imagen de f.
EJEMPLO

 Consideramos la función compleja f(z) = z + 2i z -2i. Su dominio es todos los números complejos excepto aquellos que anulan el denominador, es decir, los que verifican la ecuación z -2i = 0; por tanto, su dominio es ℂ -{2i}.
Dado que z i w = f(z) son de ℂ se pueden escribir z = x + yi y w = u + vi (descompuestos en su parte real y su parte imaginaria), podemos dar f así:
w = f(z) = u(x,y) + iv(x,y)
Por tanto, una función compleja w = f(z) equivale a tener dos funciones reales u(x,y) yv(x,y), donde cada una de ellas depende de dos variables reales x e y.

LIMITES 




CUARTA SEMANA

TEOREMA DE LIMITES DE FUNCIONES DE VARIABLE COMPLEJA

Sea w=f(z)= u(x,y)+iv(x,y) , z=x+iy ; z=xo+iyo

Si w esta definida eun una region D C C; con la posible excepcion de zo y u,v 



CONTINUIDAD




TIPOS DE DISCONTINUIDAD


SI NECESITAN MAS EXPLICACION AQUI LES DEJO UN ENLACE QUE LES SERA DE MUCHA AYUDA


http://materias.fi.uba.ar/61107/Apuntes/Vc01.pdf






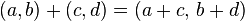
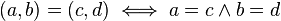
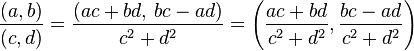
No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)